Chaotic and Memoryless Binary Sequences Based on Skew Tent Maps
0. Note
This is the second assignment from my Masters Applied Digital Information Theory Course which has never been published anywhere and I, as the author and copyright holder, license this assignment customized CC-BY-SA where anyone can share, copy, republish, and sell on condition to state my name as the author and notify that the original and open version available here.
1. Introduction
On the previous assignment we generate a chaotic sequence based on skew tent maps, and this time we generate a binary sequence (either ‘0’ or ‘1’). On this occasion we generate the chaotic binary sequence based on the threshold function.
bin = 0 if (x < c)
bin = 1 if (x ≥ c)
When a sequence value ‘x’ is less than critical point ‘c’ the binary value will be ‘0’ and when a sequence value ‘x’ is equal or greater to critical point ‘c’ the binary value will be ‘1’. For example the critical value is set as ‘c’ = 0.4 and chaotic sequence ‘x’ = [0.750000 0.416667 0.972222 0.046296 0.115741 0.289352 0.723380], the binary sequence will be ‘bin’ = [1 1 1 0 0 0 1] as Figure 1.
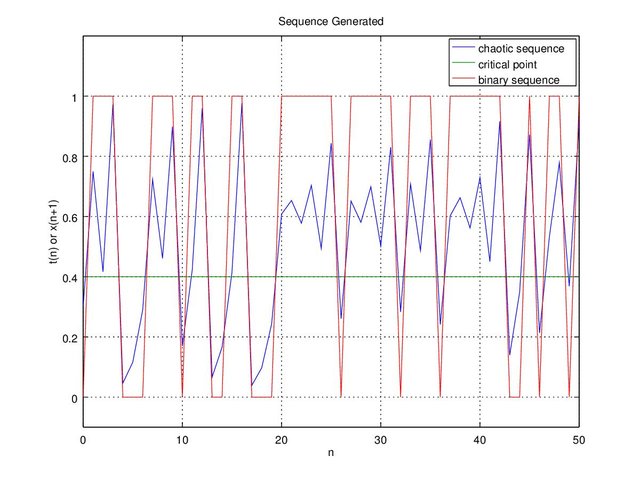
Figure 1. Chaotic binary sequence
2. Probability of binary sequence
| Using the chaotic sequence based on skew tent map to generate binary sequence we compute the probability the sequence value will be ‘0’ or ‘1’ as ‘P(0) = c’ and ‘P(1) = 1-c’. Using the skew tent map we can compute ‘P(00) = c x c’, ‘P(01) = c(1-c)’, ‘P(10) = (1-c)c’, and ‘P(11) = (1-c)(1-c)’. On Markov’s chain the probability that ‘0’ will remain ‘0’ is ‘P(0 | 0) = c’, ‘0’ will become ‘1’ is ‘P(1 | 0) = 1-c’, and so-on ‘P(0 | 1) = c’, ‘P(1 | 1) = 1-c’. |
We continue the assignment using the previous assignment to generate the binary sequence and calculate the probability of ‘0’ and ‘1’ theoretically and the actual number of ‘0’ and ‘1’ on the binary sequence generated. We used the initial value ‘x(1) = 0.3’ and trials of ‘c = 0.1, 0.2, 0.301, 0.4, 0.6, 0.7, 0.8, 0.9’. The total sequence generated is 2000000 values (2 Millions). The result is on Table 1.
Table 1. Result of theoritical calculation and actual
| Probability | Theory | Actual | Theory | Actual | Theory | Actual | Theory | Actual |
|---|---|---|---|---|---|---|---|---|
| P(0) | 0.1 | 0.100183 | 0.2 | 0.199925 | 0.301 | 0.300855 | 0.4 | 0.399797 |
| P(1) | 0.9 | 0.899817 | 0.8 | 0.800076 | 0.699 | 0.699146 | 0.6 | 0.600203 |
| P(00) | 0.01 | 0.010015 | 0.4 | 0.040114 | 0.091 | 0.090433 | 0.16 | 0.159818 |
| P(01) | 0.09 | 0.090169 | 0.16 | 0.159811 | 0.21 | 0.210422 | 0.24 | 0.239979 |
| P(10) | 0.09 | 0.090169 | 0.16 | 0.159811 | 0.21 | 0.210422 | 0.24 | 0.239979 |
| P(11) | 0.81 | 0.809649 | 0.64 | 0.640265 | 0.489 | 0.488724 | 0.36 | 0.360225 |
| P(0|0) | 0.1 | 0.999962 | 0.2 | 0.200656 | 0.301 | 0.300585 | 0.4 | 0.399757 |
| P(0|1) | 0.1 | 0.100208 | 0.2 | 0.199744 | 0.301 | 0.30097 | 0.4 | 0.39983 |
| P(1|0) | 0.9 | 0.900038 | 0.8 | 0.799354 | 0.699 | 0.699413 | 0.6 | 0.600252 |
| P(1|1) | 0.9 | 0.899792 | 0.8 | 0.800256 | 0.699 | 0.69903 | 0.6 | 0.600171 |
| Entropy | 0.46899559 | 0.46957542 | 0.72192809 | 0.72177695 | 0.88250986 | 0.88233261 | 0.97095059 | 0.97083172 |
| Filesize Original (bits) | 2000000 | 2000000 | 2000000 | 2000000 | ||||
| Filesize Compressed (bits) | 136892 | 221013 | 278698 | 312480 | ||||
| Compression Ratio | 14.61005756 | 9.049241447 | 7.176226597 | 6.400409626 | ||||
| Probability | Theory | Actual | Theory | Actual | Theory | Actual | Theory | Actual |
|---|---|---|---|---|---|---|---|---|
| P(0) | 0.6 | 0.599315 | 0.7 | 0.700161 | 0.8 | 0.800442 | 0.9 | 0.899851 |
| P(1) | 0.4 | 0.400685 | 0.3 | 0.299839 | 0.2 | 0.199559 | 0.1 | 0.10015 |
| P(00) | 0.36 | 0.359091 | 0.49 | 0.490351 | 0.64 | 0.6406 | 0.81 | 0.809735 |
| P(01) | 0.24 | 0.240225 | 0.21 | 0.209811 | 0.16 | 0.159842 | 0.9 | 0.090115 |
| P(10) | 0.24 | 0.240224 | 0.21 | 0.20981 | 0.16 | 0.159842 | 0.9 | 0.090115 |
| P(11) | 0.16 | 0.160461 | 0.09 | 0.09003 | 0.04 | 0.039718 | 0.01 | 0.010035 |
| P(0|0) | 0.6 | 0.599168 | 0.7 | 0.70034 | 0.8 | 0.800307 | 0.9 | 0.899855 |
| P(0|1) | 0.6 | 0.599535 | 0.7 | 0.699744 | 0.8 | 0.800976 | 0.9 | 0.899805 |
| P(1|0) | 0.4 | 0.400831 | 0.3 | 0.29966 | 0.2 | 0.199692 | 0.1 | 0.100144 |
| P(1|1) | 0.4 | 0.400467 | 0.3 | 0.300258 | 0.2 | 0.199027 | 0.1 | 0.1002 |
| Entropy | 0.97095059 | 0.97134988 | 0.8812909 | 0.88109401 | 0.72192809 | 0.7210441 | 0.46899559 | 0.46946961 |
| Filesize Original (bits) | 2000000 | 2000000 | 2000000 | 2000000 | ||||
| Filesize Compressed (bits) | 312428 | 278355 | 220769 | 136833 | ||||
| Compression Ratio | 6.4014749 | 7.185069426 | 9.059242919 | 14.61635717 | ||||
While the theoretical probability was calculated based on the formula, we count how much ‘0’s and ‘1’s in the sequence consist of 2 Millions binary values. For example using ‘c = 0.4’ we got 799594 ‘0’s and 1200406 ‘1’s in the 2 Millions sequence. So the actual probability of ‘0’ is ‘799594/2000000 = 0.399797’ and ‘1’ is ‘1200406/2000000 = 0.600203’. For ‘00’s is 319635, ‘01’s is 479958, ‘10’ is 479958, and ‘11’ is 720449. Everything else is on Table 1, and actual data matched the theory. For Entropy and compression ratio is discussed on the next section.
3. Entropy vs Compression Ratio
On this binary sequence we can calculate the entropy which is how much important information contained. The higher the entropy (more important information) the lower the compression ratio (the least it can be compressed). Based on Table 1 we also calculated entropy of the sequence with the following formula.
Entropy = -P(1)log2P(1) - P(0)log2P(0)
On this experiment the generated 2 million binary sequence is saved into a ‘.dat’ file. The raw file for all ‘c’ value will equal to 2MB. Here we chose to compress the ‘.dat’ file into ‘.tar.bz2’ format which is a common compression method in Linux. Finally we can plot the entropy to the compression ratio on Figure 2 which is as stated in the theory that the compression value increases with lower entropy.
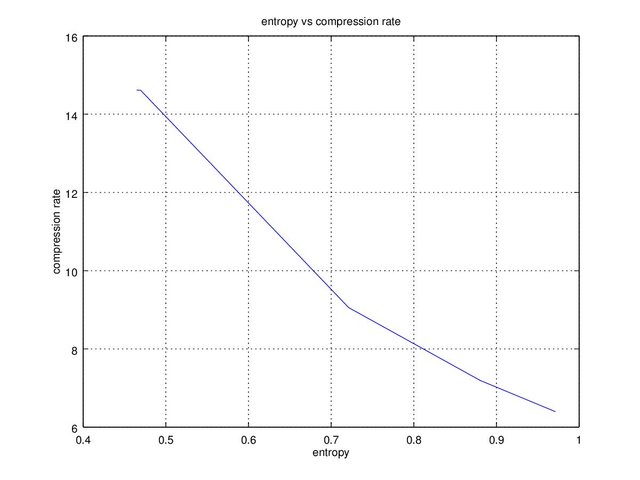
Figure 2. Entropy vs compression ratio
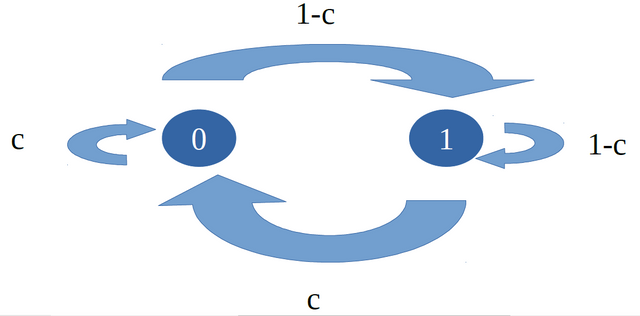
4. When t ≠ c is not memoryless
Figure 3. Markov’s Chain
When generating the binary sequence uses the threshold function bin = 0 (x < t) @ 1 ( x ≥ t), on above section it’s automatically adjust that t = c to produce a memoryless binary sequence. One of the ways to show that the binary sequence is memoryless is that it fulfills Markov’s chain on Figure 3, other than through the Bernoulli trials and independent and identically distributed (iid). We see that on table 2 that the probability is not balance, the probability of turning and remains ‘0’ should be the same, same goes for the probability of turning to 1.
Table 2. Data of t ≠ c
| x = 0.3 | c = 0.4 | x = 0.3 | t = 0.1 |
|---|---|---|---|
| P(0|0) | 0.399757 | P(0|0) | 0.396616 |
| P(0|1) | 0.39983 | P(0|1) | **0.066858** |
| P(1|0) | 0.600252 | P(1|0) | 0.603384 |
| P(1|1) | 0.600171 | P(1|1) | **0.933142** |
5. Conclusion
Using the chaotic sequence generated by skew tent map we can generate the random binary sequence with the probability of ‘0’s and ‘1’s computable. The result above shows that the theoretical probability of ‘0’s, ‘1’s, ‘00’s, ‘01’s, ‘10’s, ‘11’s, and the Markov’s chain where the probability of ‘0’ will remain ‘0’, will turn to ‘1’, ‘1’ will remain ‘1’, or turn to ‘0’ matches from the actual binary sequence generated. The theory is true to the actual. On the second case where we compare the entropy to capability of the compression, the greater the entropy the less the compression ratio. We found that the sequence is not memoryless when t ≠ c because it does not fulfill the Markov’s Chain.
6. Source Code
The script is created in Ruby language, use Ruby to run.
#!/usr/bin/ruby -w x = c = Array.new; binary_sequence = Array.new; $P0 = $P1 = $P00 = $P01 = $P10 = $P11 = $P0l0 = $P0l1 = $P1l0 = $P1l1 = 0; print "Input initial value x[1] from 0 ~ 1: "; x[1] = gets.chomp.to_f; print "\nInput critical point c[1] from 0 ~ 1: "; c = gets.chomp.to_f; print "\nInput number of sequence N: "; N = gets.chomp.to_f; for n in 1..N if x[n] >= 0 and x[n] < c x[n+1] = x[n]/c; elsif x[n] >= c and x[n] <= 1 x[n+1] = (1-x[n])/(1-c); else print "x must be from 0 ~ 1"; end end puts "P(0)_theory = c = #{c}"; puts "P(1)_theory = 1-c = #{1-c}"; puts "P(00)_theory = c*c = #{c*c}"; puts "P(01)_theory = c(1-c) = #{c*(1-c)}"; puts "P(10)_theory = (1-c)c = #{(1-c)*c}"; puts "P(11)_theory = (1-c)*(1-c) = #{(1-c)*(1-c)}"; puts "P(0|0)_theory = c = #{c}"; puts "P(0|1)_theory = c = #{c}"; puts "P(1|0)_theory = 1-c = #{1-c}"; puts "P(1|1)_theory = 1-c = #{1-c}"; puts ""; file = File.new("binary_sequence.dat", "w"); for n in 1..N if x[n] < c binary_sequence[n] = 0; $P0 += 1; elsif x[n] >= c binary_sequence[n] = 1; $P1 += 1; else print "something is wrong"; end #print binary_sequence[n]; file.syswrite(binary_sequence[n]); end P0_actual = $P0/N.to_f; P1_actual = $P1/N.to_f; for n in 1..N if binary_sequence[n] == 0 and binary_sequence[n+1] == 0 $P00 += 1; elsif binary_sequence[n] == 0 and binary_sequence[n+1] == 1 $P01 += 1; elsif binary_sequence[n] == 1 and binary_sequence[n+1] == 0 $P10 += 1; else $P11 += 1; end end P00_actual = $P00/N.to_f; P01_actual = $P01/N.to_f; P10_actual = $P10/N.to_f; P11_actual = $P11/N.to_f; P0l0_actual = P00_actual/P0_actual; P0l1_actual = P01_actual/P1_actual; P1l0_actual = P10_actual/P0_actual; P1l1_actual = P11_actual/P1_actual; puts "P(0)_actual = #{P0_actual}"; puts "P(1)_actual = #{P1_actual}"; puts "P(00)_actual = #{P00_actual}"; puts "P(01)_actual = #{P01_actual}"; puts "P(10)_actual = #{P10_actual}"; puts "P(11)_actual = #{P11_actual}"; puts "P(0|0)_actual = #{P0l0_actual}"; puts "P(0|1)_actual = #{P0l1_actual}"; puts "P(1|0)_actual = #{P1l0_actual}"; puts "P(1|1)_actual = #{P1l1_actual}"; puts ""; puts Entropy = ((-P1_actual)*(Math.log2(P1_actual)))-((P0_actual)*(Math.log2(P0_actual))); puts "Total of '0' is #{$P0}"; puts "Total of '1' is #{$P1}"; puts "Total of '00' is #{$P00}"; puts "Total of '01' is #{$P01}"; puts "Total of '10' is #{$P10}"; puts "Total of '11' is #{$P11}";
Mirrors
- https://www.publish0x.com/fajar-purnama-academics/chaotic-and-memoryless-binary-sequences-based-on-skew-tent-m-xykqpvj?a=4oeEw0Yb0B&tid=github
- https://0darkking0.blogspot.com/2021/01/chaotic-and-memoryless-binary-sequences.html
- https://0fajarpurnama0.medium.com/chaotic-and-memoryless-binary-sequences-based-on-skew-tent-maps-d3125392d0c1
- https://0fajarpurnama0.github.io/masters/2020/09/12/chaotic-and-memoryless-binary-sequences-based-on-skew-tent-maps
- https://hicc.cs.kumamoto-u.ac.jp/~fajar/masters/chaotic-real-valued-sequences-by-skew-tent-map
- https://steemit.com/math/@fajar.purnama/chaotic-and-memoryless-binary-sequences-based-on-skew-tent-maps?r=fajar.purnama
- https://stemgeeks.net/math/@fajar.purnama/chaotic-and-memoryless-binary-sequences-based-on-skew-tent-maps?ref=fajar.purnama
- https://blurtter.com/blurtech/@fajar.purnama/chaotic-and-memoryless-binary-sequences-based-on-skew-tent-maps?referral=fajar.purnama
- https://0fajarpurnama0.wixsite.com/0fajarpurnama0/post/chaotic-and-memoryless-binary-sequences-based-on-skew-tent-maps
- http://0fajarpurnama0.weebly.com/blog/chaotic-and-memoryless-binary-sequences-based-on-skew-tent-maps
- https://0fajarpurnama0.cloudaccess.host/index.php/9-fajar-purnama-academics/187-chaotic-and-memoryless-binary-sequences-based-on-skew-tent-maps
- https://read.cash/@FajarPurnama/chaotic-and-memoryless-binary-sequences-based-on-skew-tent-maps-484728ab
- https://www.uptrennd.com/post-detail/chaotic-and-memoryless-binary-sequences-based-on-skew-tent-maps~ODU0NTE5