Pembelajaran Mesin 2 Tinjauan Probabilitas
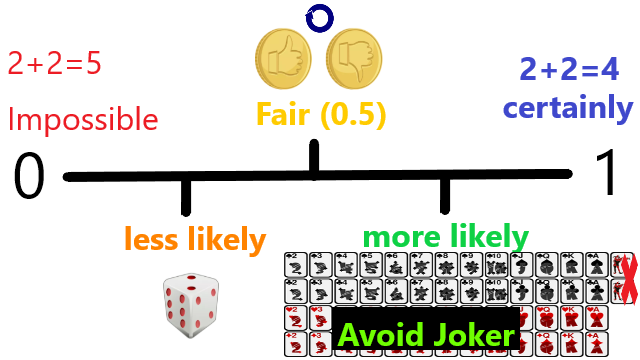
Probabilitas merupakan bagian dari matematika yang membahas kemungkinan kejadian dapat terjadi. Kemungkinan di skala dari 0 - 1 atau 0% - 100%. Dalam bahasa awam kemungkinan dapat dibagi:
- Tidak mungkin terjadi: 0 atau 0% (contohnya 2+2=5)
- Sedikit kemungkinan terjadi: ~0.25 atau ~25% (contohnya mendapat nomor genap pada dadu dan sebaliknya)
- Bisa terjadi bisa tidak terjadi: ~0.5 atau ~50% (contohnya melempar koin bisa jatuh pada bagian atas atau bawah)
- Besar kemungkinan terjadi: ~0.75 atau ~75% (contohnya dapatkan kartu angka yang ada 44 dari permainan kartu 52 komposisi)
- Pasti terjadi: 1 atau 100% (contohnya 2+2=4)
Rumus Dasar
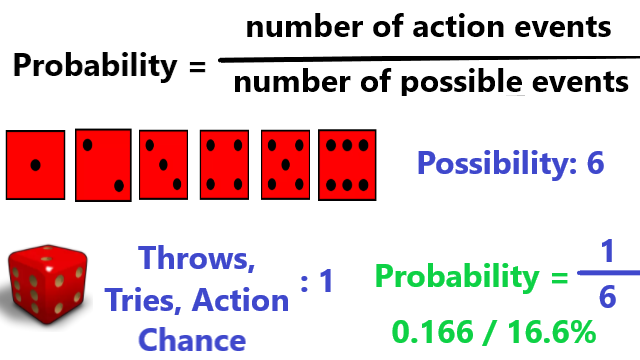
Probabilitas atau kemungkinan merupakan jumlah peristiwa dibagi dengan banyaknya cara peristiwa yang bisa terjadi. Jumlah peristiwa dapat dikaitkan dengan jumlah kesempatan, percobaan, atau aksi. Banyaknya cara peristiwa yang bisa terjadi dapat dikaitkan dengan jumlah beda hasil atau masa depan yang bisa terjadi atau dapat disingkat menjadi jumlah kemungkinan. Semakin banyak kesempatan maka semakin besar probabilitas dan semakin banyak jumlah kemungkinan semakin kecil probabilitas. Contoh pada dadu, jika melempar 1 kali, ke-6 muka dapat memiliki 1 kesempatan untuk muncul yaitu probabilitas 1/6. Jike melempar 3 kali, setiap muka memiliki 3 kesempatan untuk muncul yaitu probabilitas 3/6.
Rumus Saling Eksklusif
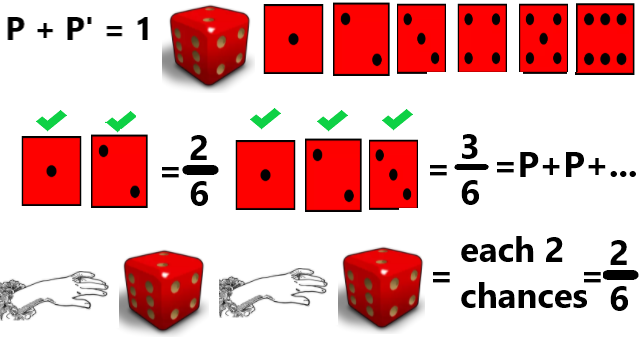
Jika masing-masing faktor, variabel, atau banyaknya cara peristiwa yang bisa terjadi tidak saling berkaitan, maka probabilitas dapat ditambah. Contohnya probabilitas munculnya angka 1 atau 2 pada dadu. Peristiwa yang diinginkan boleh angka 1, boleh angka 2, maka probabilitas adalah 1/6 + 1/6 = 2/6.
Rumus Komplemen
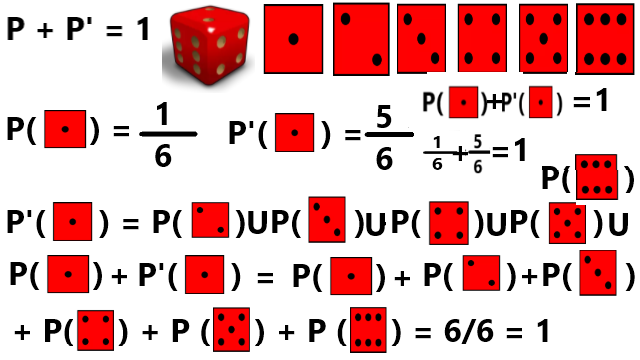
Komplemen dapat diartikan sebagai pelengkap. Jika ada probabilitas suatu peristawa akan terjadi maka ada juga probabilitas suatu peristiwa tidak akan terjadi. Kembali ke contoh dadu bila melempar 1 kali, ke-6 muka memiliki 1 kesempatan untuk muncul yaitu probabilitas 1/6. Namun setiap muka disaingi oleh 5 muka lainnya dimana salah satu dari ke-5 muka tersebut bisa muncul daripada 1 muka yang kita harapkan yaitu komplemen 5/6 atau ada 5 dari 6 kemungkinan suatu muka dadu tidak akan muncul. Peristiwa yang utuh terdiri dari probabilitas dapat terjadi dan probabilitas tidak dapat terjadi yaitu 1/6 + 5/6 = 1.
Rumus Sambungan Tidak Tergantung
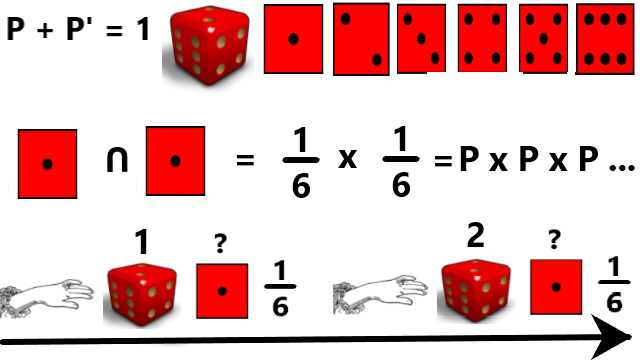
Merupakan peristiwa aksi lebih dari 1 atau peristiwa berlanjut namun tidak ada hubungannya dengan peristiwa yang terjadi sebelumnya. Misalnya melempar dadu 2 kali dan berapa probabilitas muncul untuk masing-masing angka? Peristiwa pertama adalah 1/6 dan peristiwa kedua merupakan peristawa tidak terkait atau terpisah yaitu tetap 1/6. Probabilitas munculnya angka yang kita inginkan 2 kali berturut-turut adalah 1/6 dan 1/6 adalah 1/36.
Rumus Tidak Saling Eksklusif

Bila faktor atau variabel terkait atau dalam teori set memiliki relasi dengan variabel lain maka rumus saling eksklusif akan menghasilkan duplikat dan duplikat tersebut harus dihapus. Contohnya, pemain akan menang besar bila lemparan dadu menghindari bilangan prima (1,2,3,5) atau bilangan habis akar pangkat 2 (1,4). Maka pemain akan kalah bila mendapatkan angka 1,2,3,4,5 dan menang besar bila mendapatkan angka 6. Maka probabilitas menang adalah 1/6 dan kalah adalah 5/6. Namun hasil rumus saling eklusif salah dimana pemain akan kalah bila bilangan prima 4/6 (1,2,3,5) atau bilangan habis akar pangkat 2 2/6 (1,4) dan probabilitas kalah adalah 6/6 adalah 1 yaitu pasti kalah padahal jika dapat angka 6 pemain menang. Masalah disini angka 1 juga termasuk bilangan prima dan bilangan habis akar pangkat 2 artinya duplikat. Maka harus dikurangi angka 1 duplikat tersebut (prima n habis akar pangkat 2) 1/6. Maka rumus berubah menjadi 4/6 + 2/6 - 1/6 = 5/6 kalah.
Rumus Sambungan Tergantung
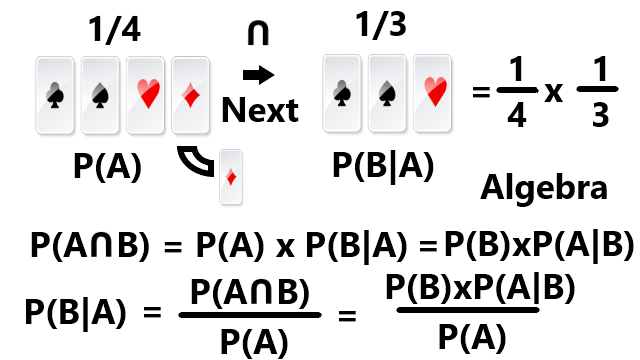
Merupakan peristiwa berlanjut dan peristiwa terkini ada hubungannya dengan peristiwa sebelumnya. Biasanya peristiwa berlanjut tapi tanpa repitisi seperti permainan kartu 52 yang dari Ace sampai Joker. Probabilitas awal adalah mengambil 1 kartu dari 52 kartu. Setelah pengambilan pertama, maka pada pengambilan kedua jumlah kartu berubah menjadi 51 kartu. Oleh karena itu probabilitas kedua yaitu 1/51.
Bayes Pembelajaran Mesin
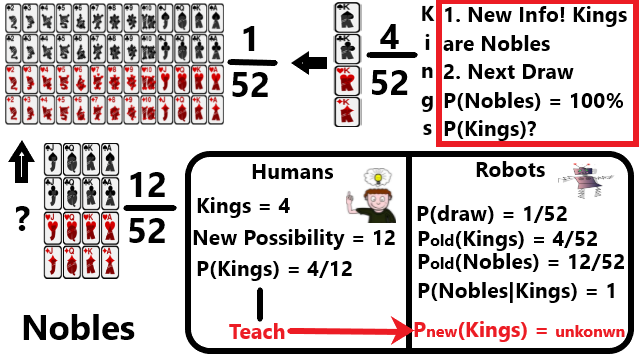
Permainan kartu 52, diketahui 2 informasi baru yaitu ke-4 raja adalah kartu bangsawan dan pengambilan kartu berikutnya dipastikan kartu bangsawan hanya ada 12. Manusia dengan langsung dapat beradaptasi dan langsung tahu bahwa probabilitas raja adalah 4/12. Bagaimana dengan robot? Robot hanya tahu ada 4 raja dari 52 kartu (4/52) harus diajarkan oleh manusia. Bagaimana agar robot bisa belajar sendiri? Ajarkan rumus Bayes:
| P(penyebab | akibat) = P(akibat | penyebab) * P(penyebab) / P(akibat) |
| P(akibat | penyebab) = P(penyebab | akibat) * P(akibat) / P(penyebab) |
P(akibat) = P(raja) = 4/52
P(penyebab) = P(bangsawan) = 12/52
| P(penyebab | akibat) = P(jika muncul raja maka pasti bangsawan) = P(bangsawan | raja) = 1 |
| Robot akan menghitung berapa probabilitas raja jika informasi sebelumnya adalah kartu bangsawan = P(akibat | penyebab) = P(raja | bangsawan) |
| P(raja | bangsawan) = P(bangsawan | raja) * P(raja) / P(bangsawan) = 1 * (4/52) / (12/52) = (4/52) * (52/12) = 208/624 = 4/12 (terbukti) |
Masih Banyak Yang Lain
- Distribusi Probabilitas
- Product Rules
- Chain Rules
- Random Variables
- Markov Decision Process
- Hidden Markov Model
- Naive Bayes
- Laten Dirchlet Allocation
- Conditional Random Field
- Decision Networks