Opacity: zIndex: Get 100000 0FP0EXP Token to input your own list (json format) or insert json link:

Get 80000 0FP0EXP Token to input your own list (json format) or insert json link:

My Playlist:

JSON Ready: Not Ready

Ready State:

Network State:

Name:

Album:

Reference:

Background Color

General HTML background color:

Header background color:

Menu background color:

Content background color:

Widget background color:

Footer background color:

Font Size

Get 150000 0FP0EXP Token to unlock this feature.

Heading 1 font size:

Heading 2 font size:

Heading 3 font size:

Heading 4 font size:

Heading 5 font size:

Heading 6 font size:

Header font size:

Header Widget font size:

Menu font size:

Widget font size:

Footer font size:

Content font size:

Font Color

Get 200000 0FP0EXP Token to unlock this feature.

Heading 1 font color:

Heading 2 font color:

Heading 3 font color:

Heading 4 font color:

Heading 5 font color:

Heading 6 font color:

Header font color:

Header Widget font color:

Menu font color:

Widget font color:

Footer font color:

Content font color:

Font Shadow

Get 250000 0FP0EXP Token to unlock this feature.

Heading 1 font shadow:

Heading 2 font shadow:

Heading 3 font shadow:

Heading 4 font shadow:

Heading 5 font shadow:

Heading 6 font shadow:

Header font shadow:

Header Widget font shadow:

Menu font shadow:

Widget font shadow:

Footer font shadow:

Content font shadow:

Other Styles Coming Soon

Source Code

Click the above image for basic sourced and click following button for processing token source code.

Ethereum Virtual Machine

Ethereum and EVM (ETC, BSC, AVAX-C-Chain, Polygon, etc).

Telegram Open Network

Telegram Open Network (TON) decentralized application.

Solana

Solana decentralized application.

Tron

Tron decentralized application.

Near

Near decentralized application.

Wax

Wax decentralized application.

Myalgo

Myalgo wallet for Algorand decentralized application.

Sync2

Sync2 wallet for Vechain decentralized application.

Scatter

Scatter wallet for EOS decentralized application.

Ontology

Ontology decentralized application.

Rabbet

Rabbet wallet for Stellar Lumen decentralized application.

Freighter

Freighter wallet for Stellar Lumen decentralized application.

Hivesigner

Hive Signer for Hive decentralized application.

Hivekeychain

Hive Key Chain for Hive decentralized application.

Zilpay

Zilpay wallet for Zilliqa decentralized application.

Neoline N2

Neoline wallet for Neo N2 decentralized application.

Neoline N3

Neoline wallet for Neo N3 decentralized application.

Keplr

Keplr wallet for Cosmos and other decentralized application.

Keeper

Keeper wallet for Waves decentralized application.

IWallet

IWallet for IOST decentralized application.

Financial Technical Analysis Crypto Narrative Chapter 7 Harmonic Pattern

Get 60 0FP0EXP Token to remove widget entirely!

source code



source code
old source code

get any 0FP0EXP Token to automatically turn off or 10 0FP0EXP Token to remove this JavaScript Mining.

Get 50000 0FP0EXP Token to remove my NFTS advertisements!

Get 40000 0FP0EXP Token to remove this donation notification!

get 30000 0FP0EXP Token to remove this paypal donation.

View My Stats

Need referral links?

get 20000 0FP0EXP Token to remove my personal ADS.

word number: 1848

Time: 2024-10-02 15:37:44 +0000

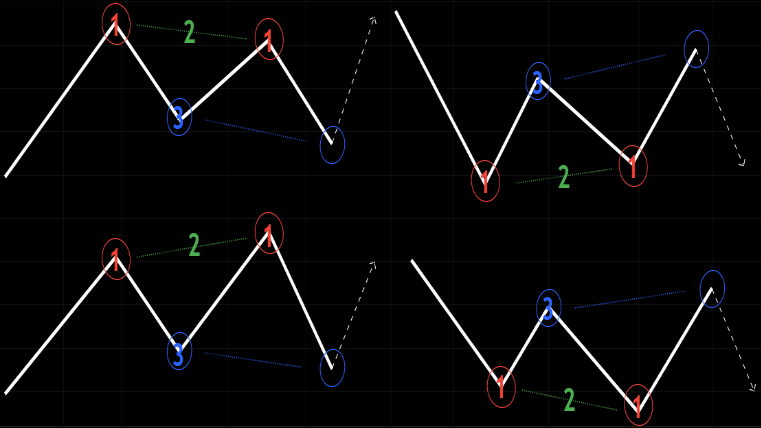
0.harmonic-pattern.png

In Chapter 5, we draw lower and upper trend line to identify classic chart patterns but in this chapter we use Chapter 6 Fibonnaci Golden Ratios to measure harmonic chart patterns. Most harmonic patterns have 5 phases forming XABCD pattern. To quickly identify them is to find 2 mountains for bullish harmonic patterns and 2 wells for bearish harmonic patterns. The next thing to see is whether one of the mountains or wells is shorter than the other. Finally, the middle point is higher than the first and last point for bullish harmonic patterns and lower than the first and last point for bearish harmonic patterns. In short should look similar to an imperfect “M” letter for bullish harmonic patterns and imperfect “W” letter for bearish harmonic patterns.

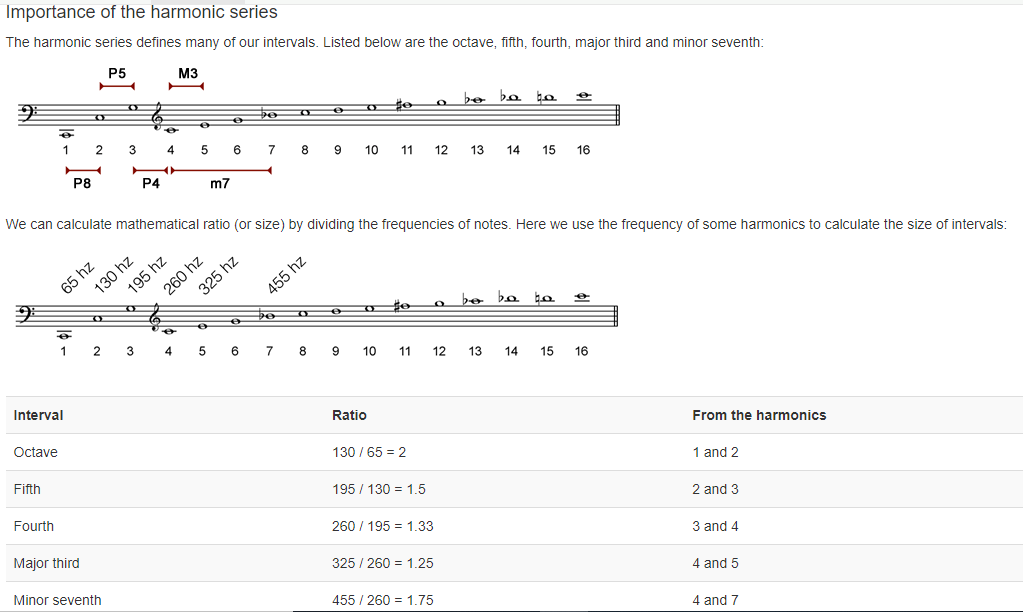
1.harmonic-series.PNG

The harmonic patterns are said to be inspired from music and wave theories of harmonic ratios. For example from José Rodríguez Alvira, Harmonic Series, an Octave have a ratio of 130 Hz / 65 Hz = 2. Harmonic patterns are defined by the measurements of Fibonacci Golden Ratios on the XABCD pattern.

Measuring Harmonic Patterns

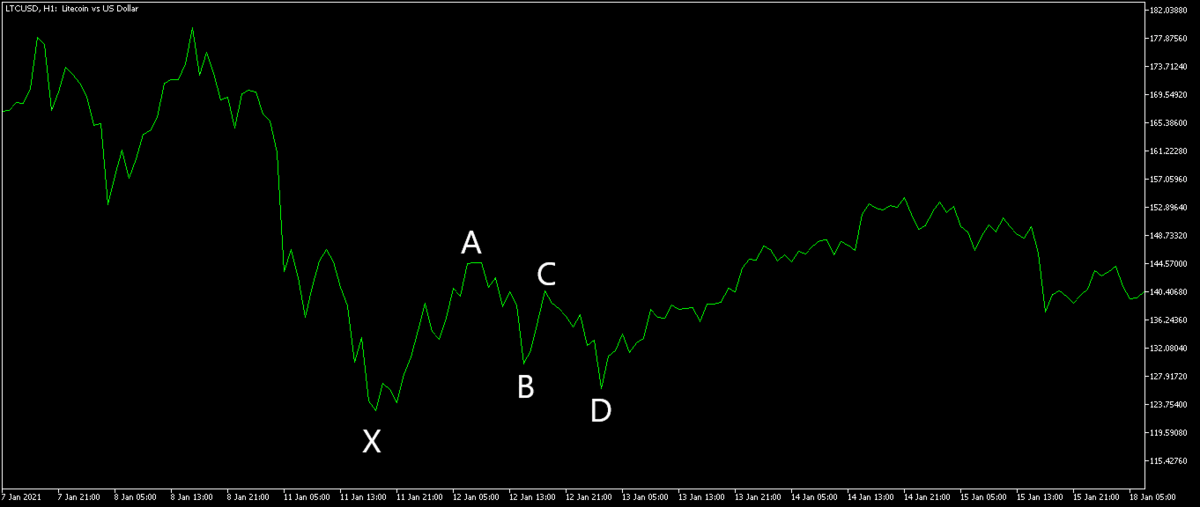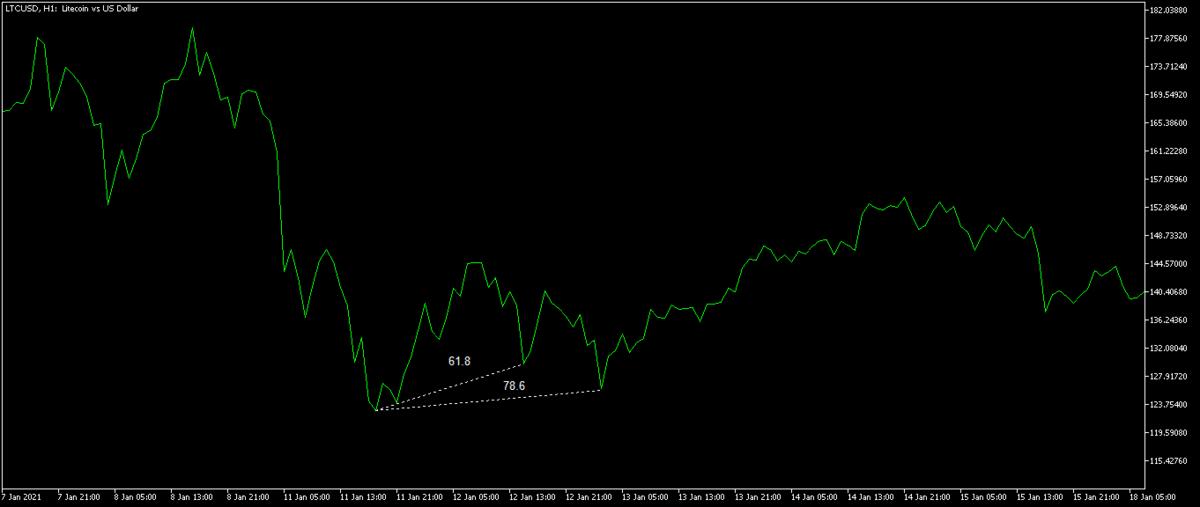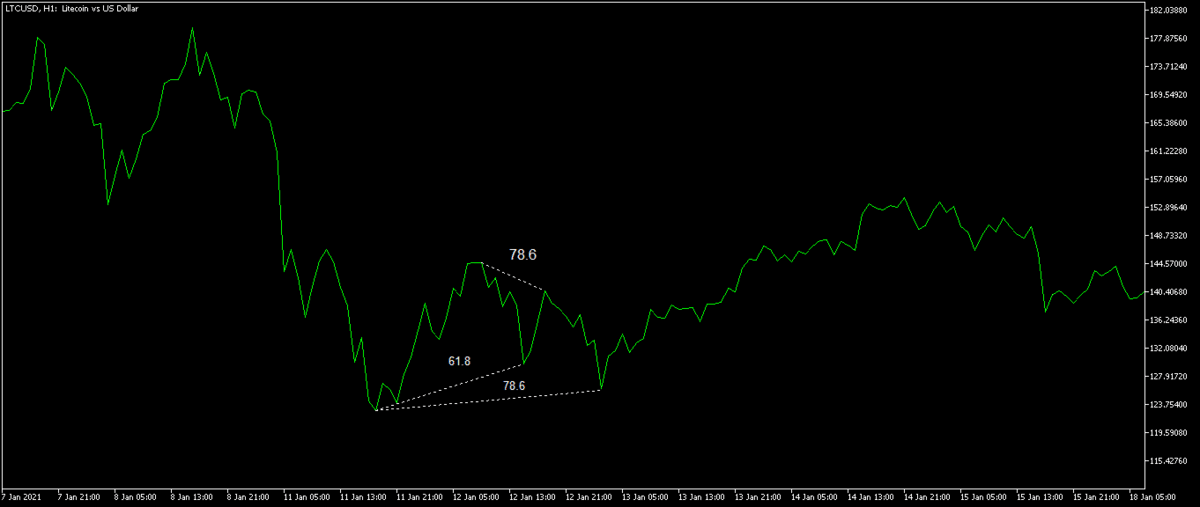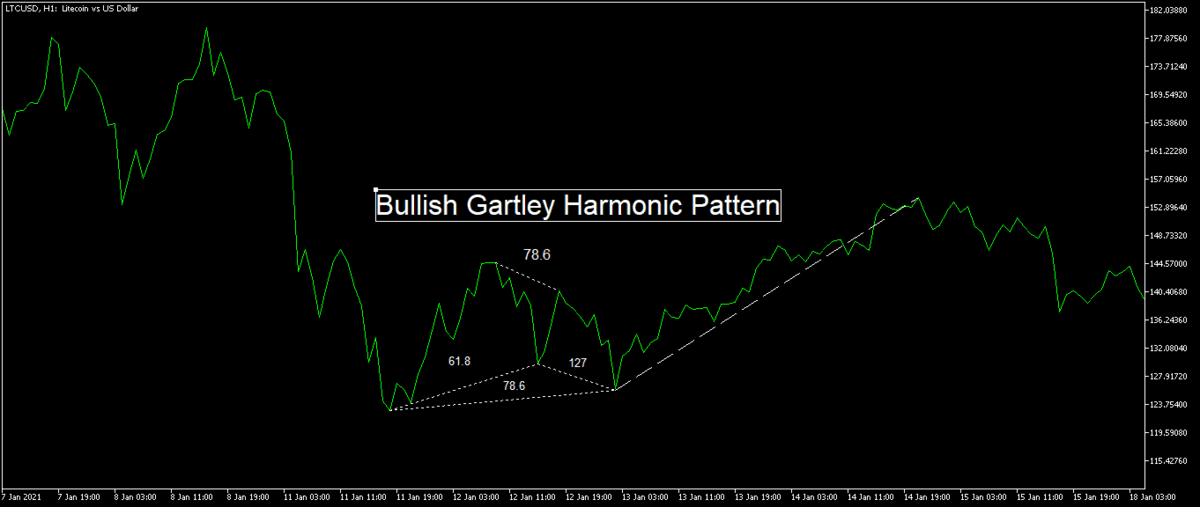
2.draw-manual.gif

To measure a harmonic pattern after identifying one:

  1. Label the XABCD points.
  2. Pull a Fibonacci Retracement from X to A to get XB and XD parameter.
  3. Pull a Fibonacci Retracement from A to B to get AC parameter.
  4. Pull a Fibonacci Retracement from B to C to get XAB or XB ratio.

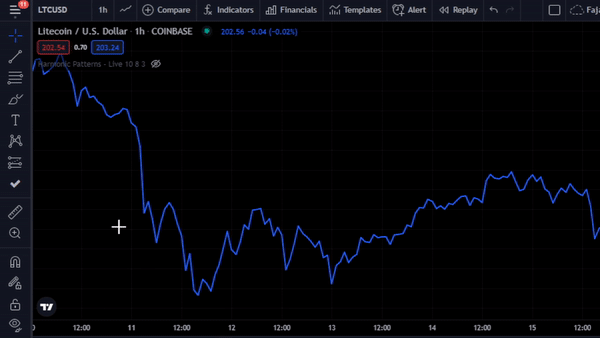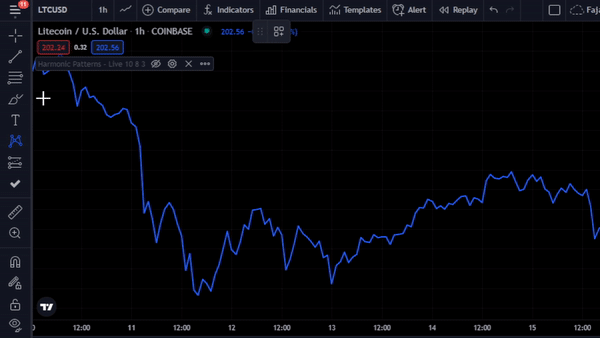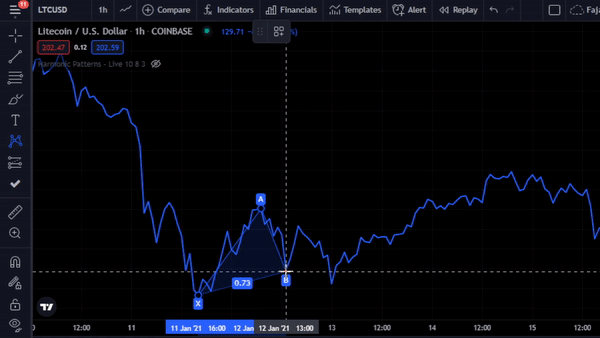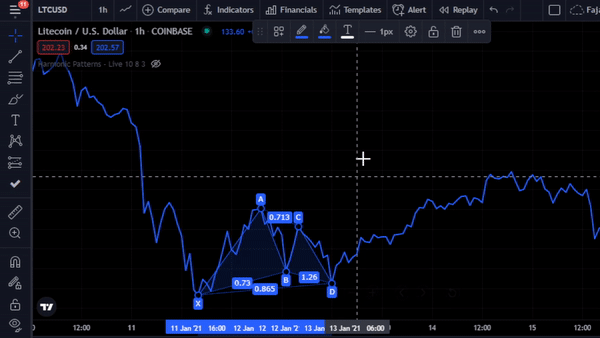
3.xabcd-tool.gif

In trading view, there is XABCD pattern tool where we do not need to measure manually like the previous steps for example in Metatrader. For upcoming trades, harmonic traders predicts the next Fibonacci Retracement Golden Ratio. Then they put a buy or sell limit with a certain stop loss percentage for example 5%. The previous examples are Bullish Gartley harmonic pattern. I found the Forex market having very precise Fibonacci Golden Ratio numbers when harmonic pattern occurs but not so precise with the cryptocurrency market especially if we use the candle’s shadow instead of the closing price. This is probably because the market capitulation is still not high enough in cryptocurrency to suppress many market manipulation. Therefore, expect certain degree of tolerance in the Fibonacci Retracement measurements.

Gartley Harmonic Pattern

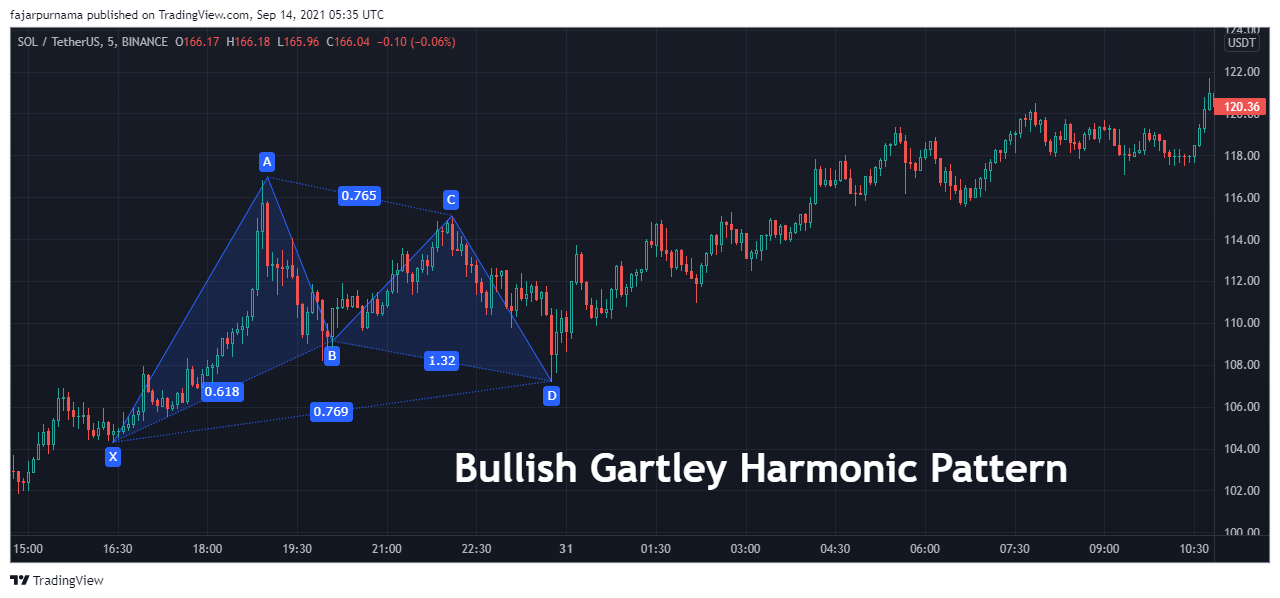
4a.bullish-gartley.png

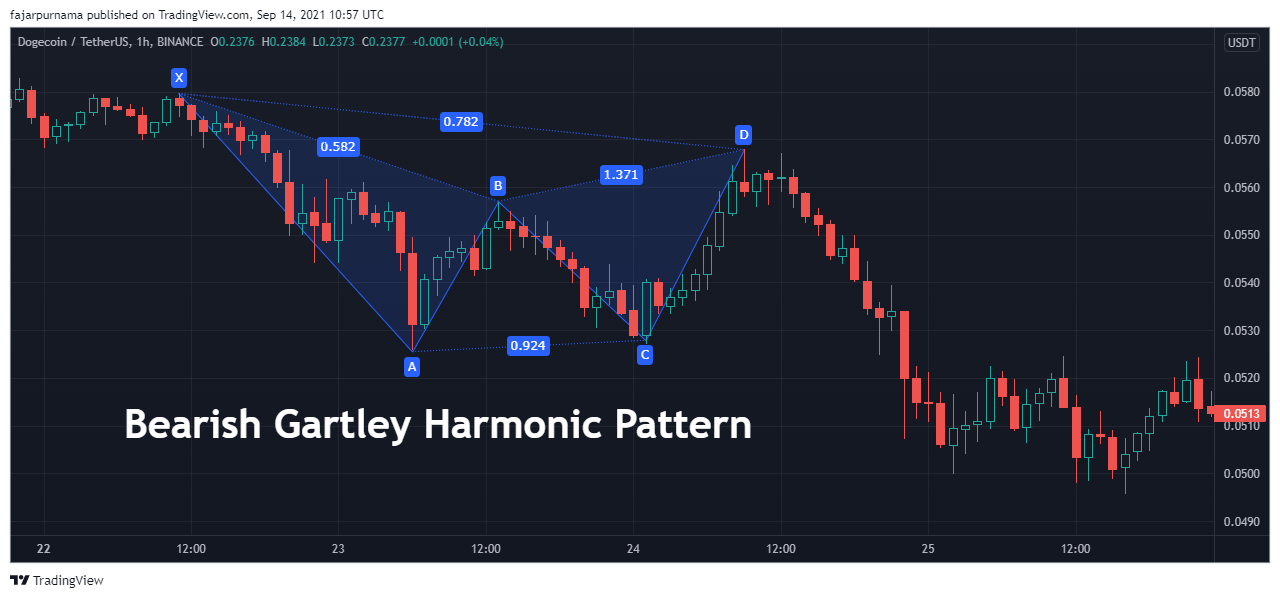
4b.bearish-gartley.png

The most popular harmonic pattern is Gartley. After the impulsive phase, there are no extreme price fluctuation in the correction phase. The Fibonacci Golden Ratios are as below:

  • XB: 0.618
  • AC: 0.382 - 0.886
  • BD: 1.272 - 1.618
  • XD: 0.786

Bat Harmonic Pattern

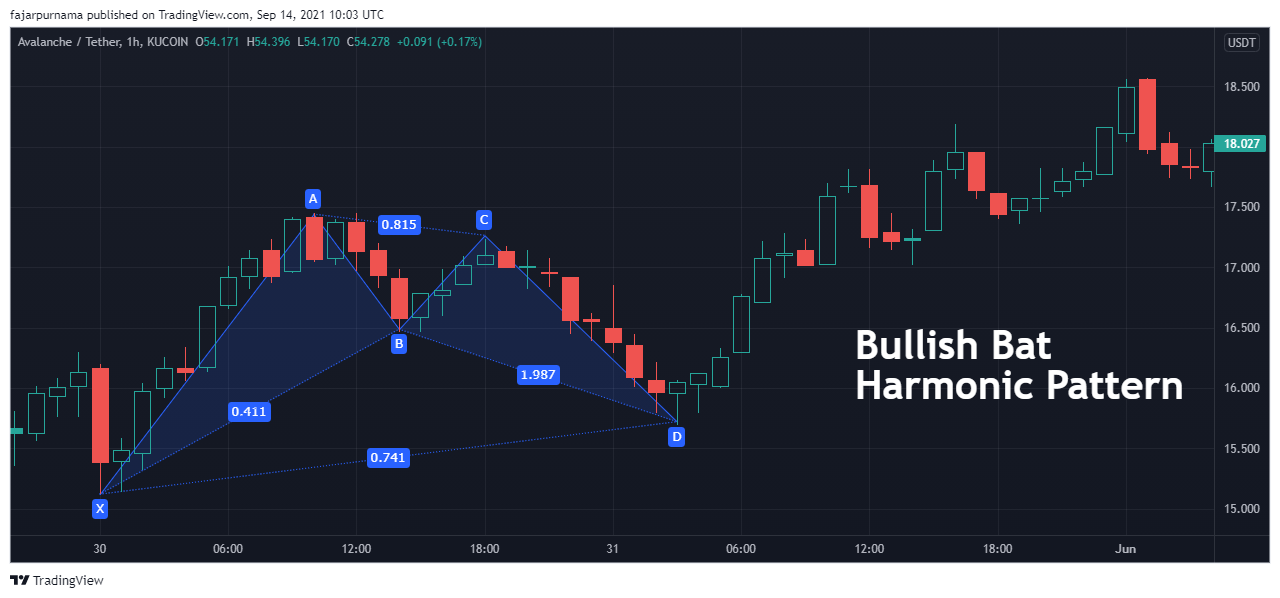
5a.bullish-bat.png

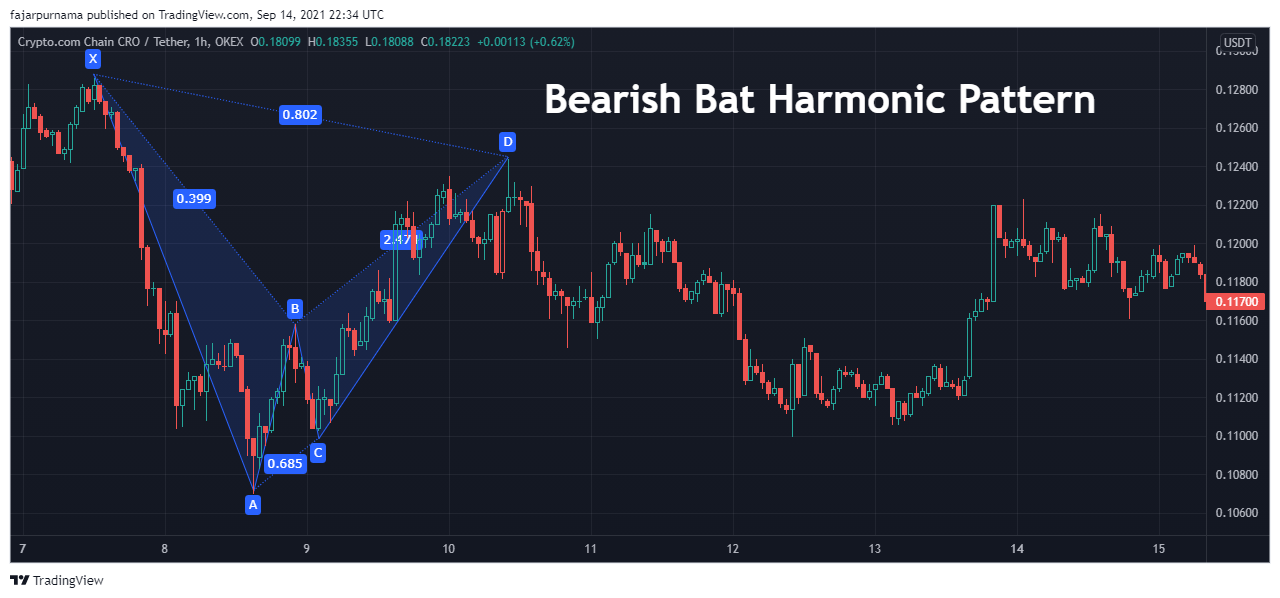
5b.bearish-bat.png

Bat harmonic pattern looks like a bat’s wings which are long but narrow. The distance between the middle and the first and the last points are long while the distance between the middle and its neighboring points are short. The Fibonacci Golden Ratios are as below:

  • XB: 0.382 - 0.5
  • AC: 0.382 - 0.886
  • BD: 1.618 - 2.618
  • XD: 0.886

Butterfly Harmonic Pattern

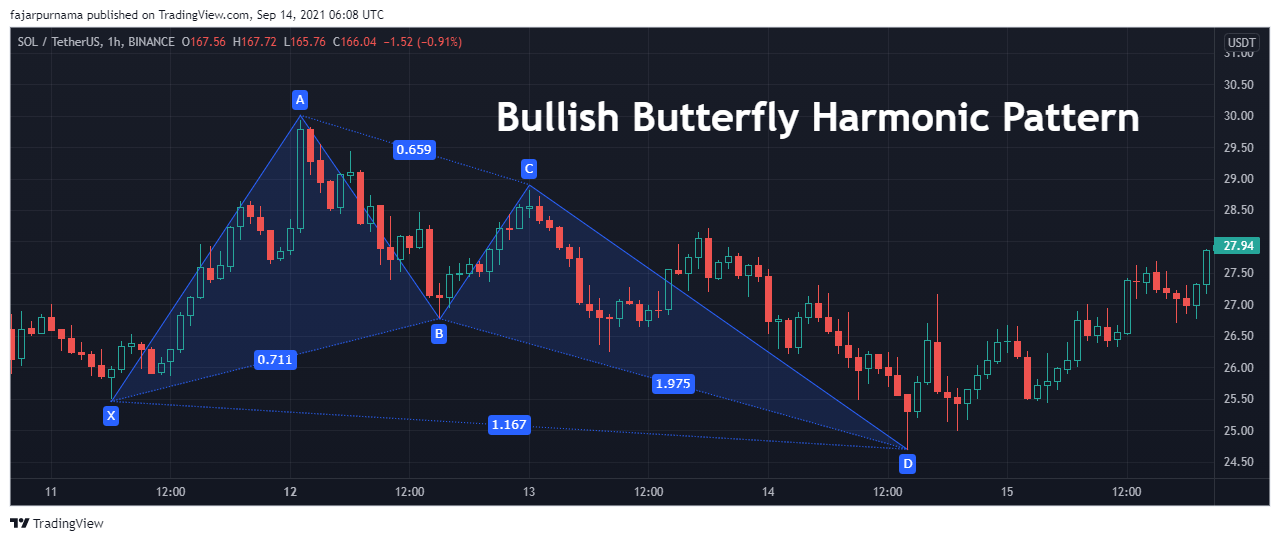
6a.bullish-butterfly.png

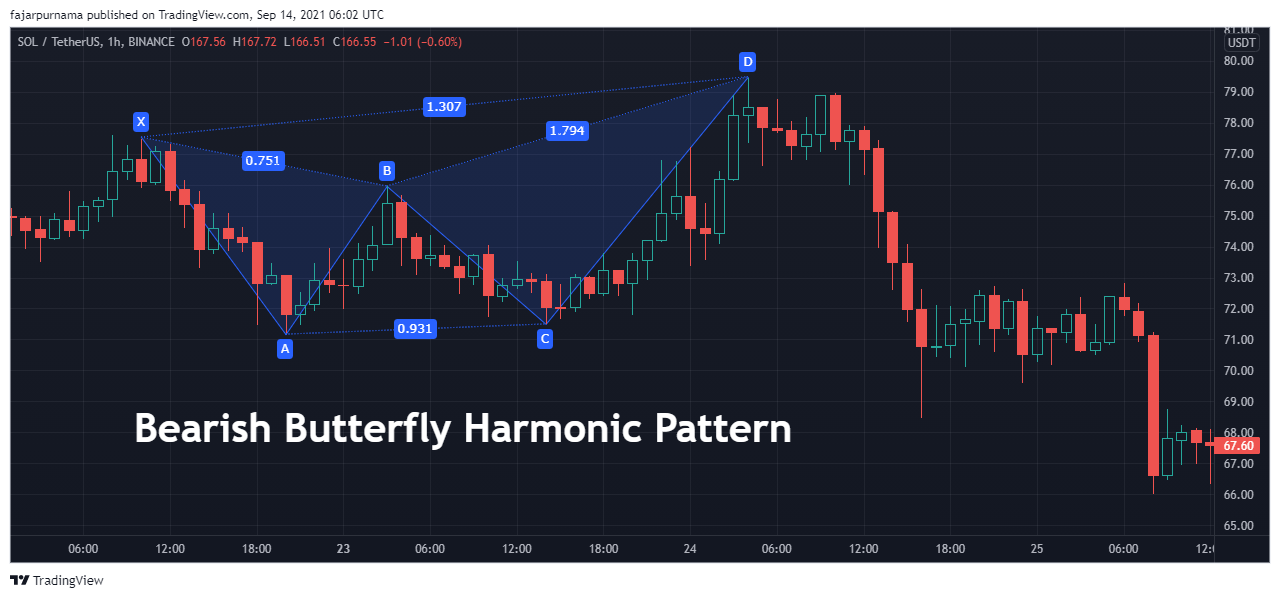
6b.bearish-butterfly.png

Butterfly harmonic pattern looks like a butterfly’s wings. While in Gartly, one of the wing is smaller than the other but in Butterfly the last point breaks the price line of the first point making both wings equal. The Fibonacci Golden Ratios are as below:

  • XB: 0.786
  • AC: 0.382 - 0.886
  • BD: 1.618 - 2.618
  • XD: 1.272 - 2.618

Crab Harmonic Pattern

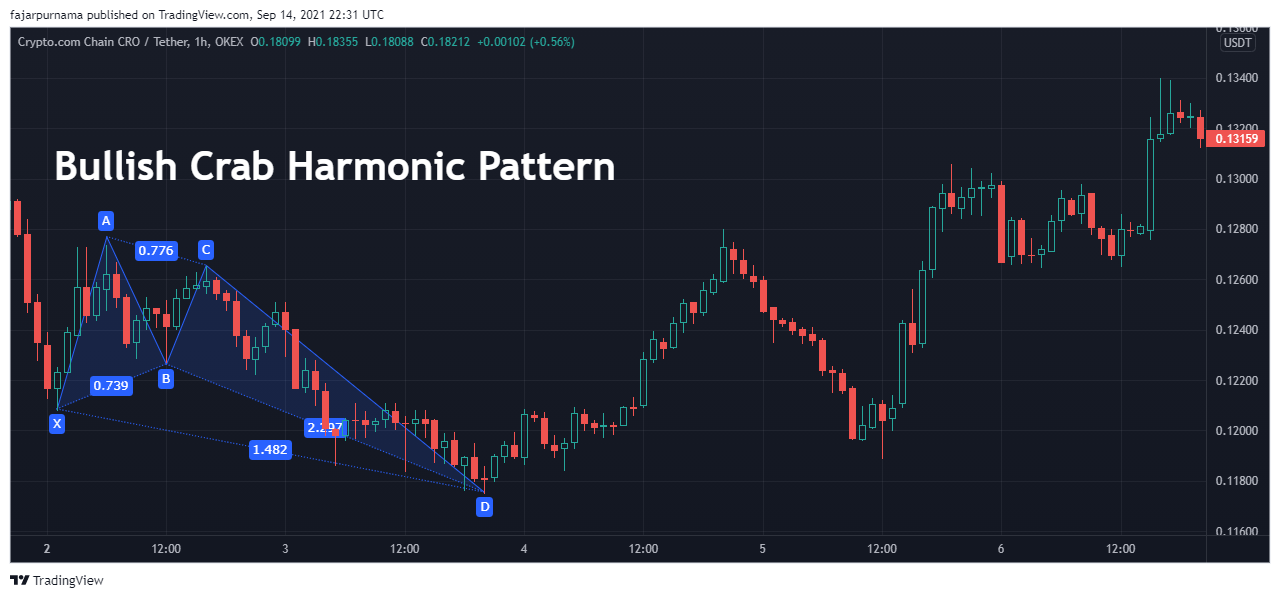
7a.bullish-crab.png

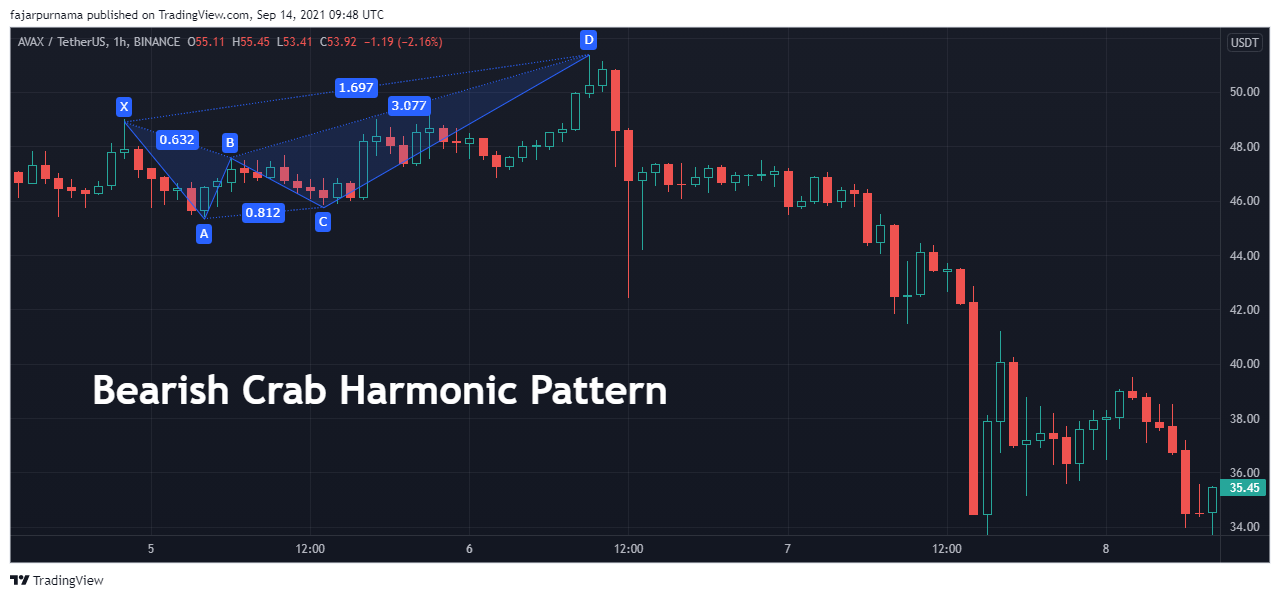
7b.bearish-crab.png

I do not know why they call this the Crab Harmonic Pattern. Maybe because crabs walks sideways and their pinches which is represented by one of its side longer then the other? The Fibonacci Golden Ratios are as below:

  • XB: 0.382 - 0.618
  • AC: 0.382 - 0.886
  • BD: 2.24 - 3.618
  • XD: 1.618

Some Other Harmonic Patterns

New Cypher Harmonic Pattern

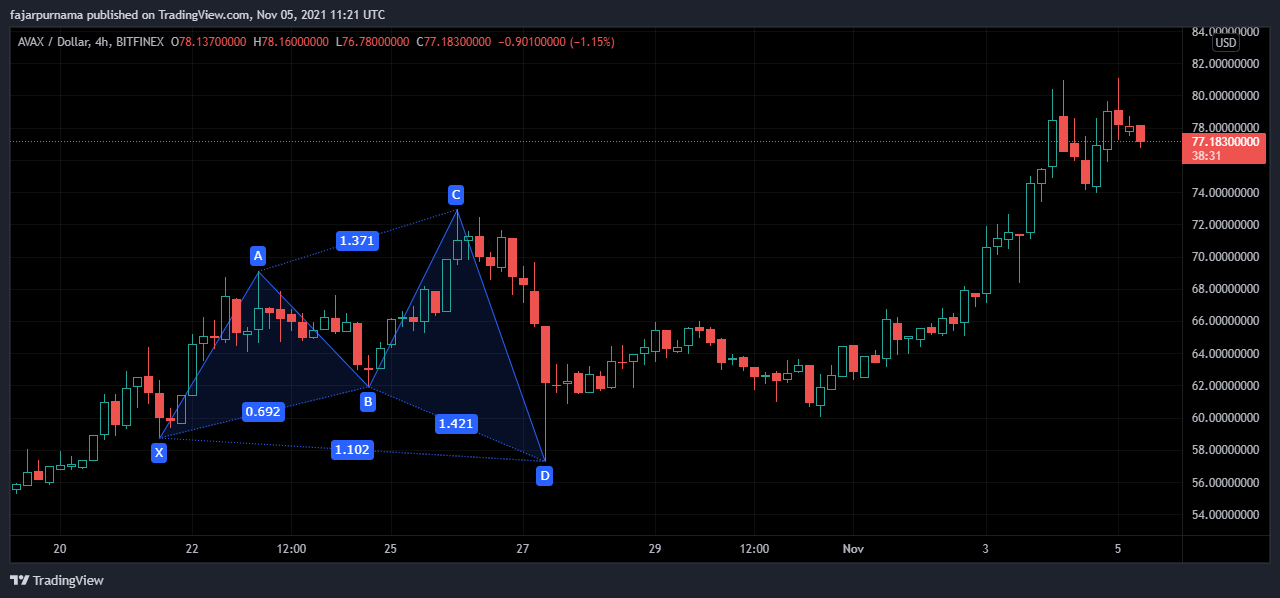
8a.bullish-new-cypher.png

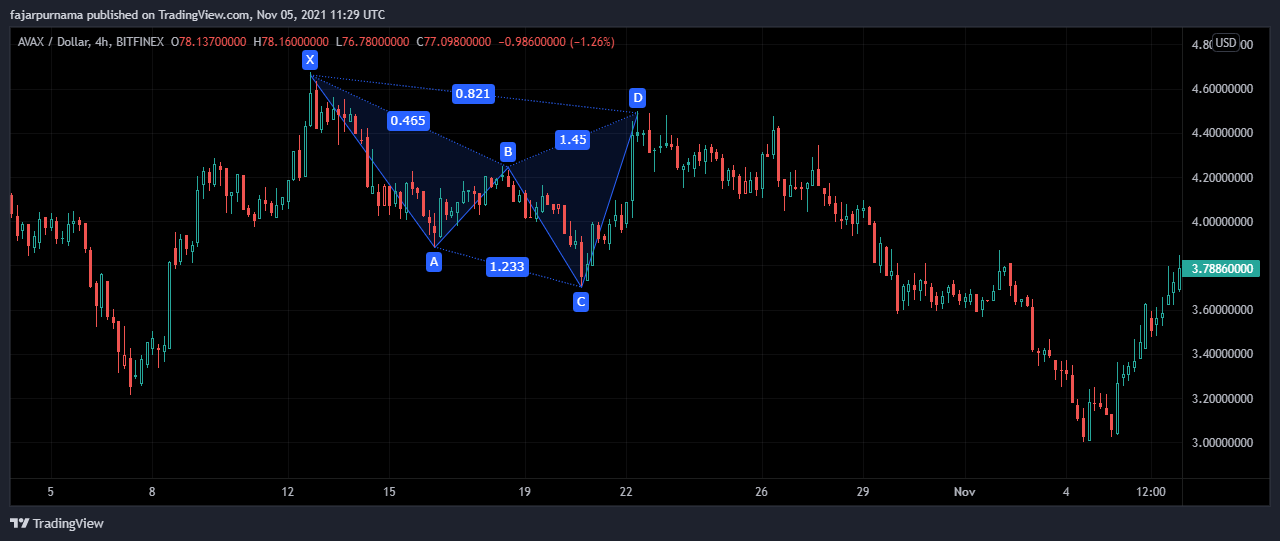
8b.bearish-new-cypher.png

The new cypher harmonic pattern I see as the reverse mountains, reverse wings, or reverse sides of any harmonic patterns where usually the left side is higher than the right side, here the right side is higher.

More Lists

Source: http://chartreaderpro.com/harmonic-pattern-ratios/.

Name XB AC BD XD
Max Bat 0.382 - 0.618 0.382 - 0.886 1.272 - 2.618 0.886
Max Gartley 0.382 - 0.618 0.382 - 0.886 1.128 - 2.236 0.618 - 0.786
Alt Shark 2 0.446 - 0.618 0.618 - 0.886 1.618 - 2.618 0.886
Anti Nen star 0.5 - 0.786 0.467 - 0.707 1.618 - 2.618 0.786
Leonardo 0.5 0.382 - 0.886 1.128 - 2.618 0.786
Anti New Cypher 0.5 - 0.786 0.467 - 0.707 1.618 - 2.618 1.272
Max Butterfly 0.618 - 0.886 0.382 - 0.886 1.272 - 2.618 1.272 - 1.618
Butterfly 113 0.786 - 1 0.618 - 1 1.128 - 1.618 1.128
Alt Shark 1 0.446 - 0.618 0.618 - 0.886 1.618 - 2.618 1.128
Deep Crab 0.886 0.382 - 0.886 2.618 - 3.618 1.618
A Crab 0.276 - 0.446 1.128 - 2.618 1.618 - 2.618 0.618
New Cypher 0.382 - 0.618 1.414 - 2.14 1.272 - 2 0.786
A Butterfly 0.382 - 0.618 1.128 - 2.618 1.272 0.618 - 0.786
Shark 1 0.382 - 0.618 1.128 - 1.618 1.618 - 2.236 0.886
A Bat 0.382 - 0.618 1.128 - 2.618 2 - 2.618 1.128
Shark 2 0.382 - 0.618 1.128 - 1.618 1.618 - 2.236 1.128
Nen star 0.382 - 0.618 1.414 - 2.14 1.272 - 2 1.272
Alt Bat 0.382 0.382 - 0.886 2 - 3.618 1.128
Navarro 200 0.382 - 0.786 0.886 - 1.128 0.886 - 3.618 0.886 - 1.128
A Gartley 0.618 - 0.786 1.128 - 2.618 1.618 1.272
121 0.5 - 0.786 1.128 - 3.618 0.382 - 0.786 0.382 - 0.786
White Swan 0.382 - 0.786 2 - 4.237 0.5 - 0.886 0.238 - 0.886
A 3 Drives 0.618 - 0.786 1.272 - 1.618 0.618 - 0.786 0.13 - 0.886
Partizan 2 0.128 - 3.618 1.128 - 1.618 1.618 - 2.236 0.618 - 3.618
A 121 1.272 - 2 0.5 - 0.786 1.272 - 2 1.272 - 2.618
3 Drives 1.272 - 1.618 0.618 - 0.786 1.272 - 1.618 1.618 - 2.618
Black swan 1.382 - 2.618 0.236 - 0.5 1.128 - 2 1.128 - 2.618
HENRY – David 0.128 - 2 0.44 - 0.618 0.618 - 0.886 0.618 - 1.618
STRONG HENRY –
David		 0.128 - 2.618 0.44 - 0.618 0.618 - 0.886 0.618 - 1.618
May-00 1.128 - 1.618 1.618 - 2.236 0.5 - 0.618 0.5 - 0.618
DAVID VM 1 0.128 - 1.618 0.382 1.618 0.618 - 3.618
DAVID VM 2 1.618 - 3.618 0.382 1.618 0.618 - 7.618
SNORM 0.9 - 1.1 0.9 - 1.1 0.9 - 1.1 0.618 - 1.618
COL Poruchik 0.128 - 3.618 0.382 - 2.618 1 0.618 - 3.618
Sea Pony 0.128 - 3.618 0.382 - 0.5 1.618 - 2.618 0.618 - 3.618
Partizan 0.128 - 3.618 0.382 1.618 0.618 - 3.618
TOTAL 1 0.382 - 0.786 0.382 - 0.886 1.272 - 2.618 0.786 - 0.886
TOTAL 2 0.382 - 0.786 0.382 - 0.886 1.618 - 3.618 1.128 - 1.618
TOTAL 3 0.276 - 0.618 1.128 - 2.618 1.272 - 2.618 0.618 - 0.886
TOTAL 4 0.382 - 0.786 1.128 - 2.618 1.618 - 2.618 1.128 - 1.272
TOTAL 0.276 - 0.786 0.382 - 2.618 1.272 - 3.618 0.618 - 1.618
Partizan 2.1 0.128 - 3.618 1.128 1.618 0.618 - 3.618
Partizan 2.2 0.128 - 3.618 1.128 2.236 0.618 - 3.618
Partizan 2.3 0.128 - 3.618 0.618 - 1.618 1.618 0.618 - 3.618
Partizan 2.4 0.128 - 3.618 1.618 2.236 0.618 - 3.618
BG1 0.128 - 0.886 0.618 1.618 1
BG2 0.128 - 0.886 0.707 1.414 1
BG3 0.128 - 0.886 0.786 1.272 1
BG4 0.128 - 0.886 0.886 1.128 1
BG5 0.128 - 0.886 0.5 2 1
BG1 0.128 - 0.886 0.382 2.618 1
BG2 0.128 - 0.886 0.447 2.237 1
BG3 0.128 - 0.886 0.5 2 1
BG4 0.128 - 0.886 0.618 1.618 1
BG5 0.128 - 0.886 0.707 1.414 1
BG6 0.128 - 0.886 0.786 1.272 1
BG7 0.128 - 0.886 0.854 1.171 1
BG8 0.128 - 0.886 0.886 1.128 1
121 BG 0.5 - 0.577 1.128 - 1.733 0.618 - 0.707 0.447 - 0.786
NN Gartley 0.618 0.382 - 0.886 1.128 - 1.618 0.786
NN Bat 0.382 - 0.5 0.382 - 0.886 1.618 - 2.618 0.886
NN Alt Bat 0.382 0.382 - 0.886 2 - 4.236 1.128
NN Crab 0.382 - 0.618 0.382 - 0.886 2.236 - 4.236 1.618
NN Deep Crab 0.886 0.382 - 0.886 2.618 - 4.236 1.618
NN A Gartley 0.618 - 0.786 1.128 - 2.618 1.618 1.272
NN A Bat 0.382 - 0.618 1.128 - 2.618 2 - 2.618 1.128
NN A Alt Bat 0.236 - 0.5 1.128 - 2.618 2.618 0.886
NN A Butterfly 0.382 - 0.618 1.128 - 2.618 1.272 0.618 - 0.786
NN A Crab 0.236 - 0.447 1.128 - 2.618 1.128 - 2.618 0.618
NN A Deep Crab 0.236 - 0.382 1.128 - 2.618 1.128 0.618
NN Leo 0.5 0.382 - 0.886 1.128 - 2.618 0.786
NN A Leo 0.382 - 0.886 1.128 - 2.618 2 1.272
NN Total 1 0.382 - 0.786 0.382 - 0.886 1.272 - 2.618 0.786 - 0.886
NN Total 2 0.382 - 0.786 0.382 - 0.886 1.618 - 4.236 1.128 - 1.618
NN Total 3 0.236 - 0.618 1.128 - 2.618 1.272 - 2.618 0.618 - 0.886
NN Total 4 0.382 - 0.786 1.128 - 2.618 1.618 - 2.618 1.128 - 1.272
NN TOTAL *** 0.236 - 0.786 0.382 - 2.618 1.272 - 4.236 0.618 - 1.618
NN Bl Swan 1.382 - 2.618 0.236 - 0.5 1.128 - 2 1.128 - 2.618
NN Wh Swan 0.382 - 0.724 2 - 4.236 0.5 - 0.886 0.382 - 0.886

Mirrors